V tomto článku se budeme zabývat objemovou parametrizací hydraulického profilu přímoproudé Kaplanovy turbíny. Její geometrický popis, který je závislý na několika parametrech, je uveden v předchozím článku a bude určovat hraniční plochy pro výpočet B-spline/NURBS objemové parametrizace.
Vzhledem ke složitosti tvaru Kaplanovy turbíny (zejména pasáží obsahující rozváděcí nebo oběžné lopatky) byl geometrický model Kaplanovy turbíny rozdělen na několik částí:
- lopatkový kanál,
- vstupní kanál,
- prostor s rozváděcími lopatkami,
- mezilopatková část,
- prostor s oběžnými lopatkami,
- savka s částí náboje.
U každé z těchto částí následně určíme objemovou parametrizaci. Jednotlivé objemy mají společné hraniční plochy ve směru osy turbíny, avšak řídící sítě příp. uzlové vektory těchto společných hraničních ploch mohou být odlišné. Odlišnost popisu hraničních ploch může být komplikací při použití těchto objemů pro isogeometrickou analýzu, tuto situaci lze však vyřešit s použitím tzv. nekonformních NURBS sítí.
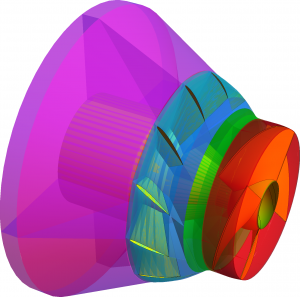
Při určování objemových parametrizací jednotlivých segmentů jsme využili dvě různé metody. První z nich využívá toho, že daný hraniční útvar tvoří rotační těleso, a proto lze řídící síť dourčit pomocí NURBS popisu kružnice. Naopak druhý způsob je o něco komplikovanější, jedná se o metodu, kdy vstupem jsou plochy tvořící obecný šestistěn a cílem je dourčit vnitřní řídící body (zejména pomocí diskrétního Coonsova plátu) tak aby vstupní šestistěn byl hranicí výsledného B-spline/NURBS objemu. Jelikož v našem případě jsou některé hraniční plochy pláty na sféře, budeme k určení těchto ploch používat sférickou projekci. Na následujícím obrázku jsou ukázány vytvořené objemy lopatkového kanálu Kaplanovy turbíny.
Vzhledem k tomu, že výsledné B-spline/NURBS objemy budou vstupem do isogeometrického řešiče, jenž je citlivý na počáteční data, bylo nutné snažit se o objemové parametrizace nízkých stupňů (max. stupeň 3) s co nejmenším počtem řídících bodů (problém zejména u objemu s oběžnými lopatkami). Z důvodu citlivosti řešiče na vstupní data předpokládáme, že některé části bude možná nutné optimalizovat (např. aproximovat některé racionální objemy pomocí polynomiálních).