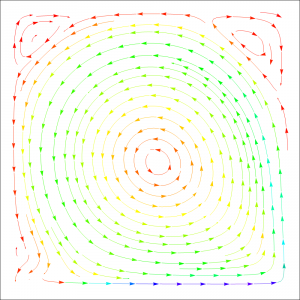
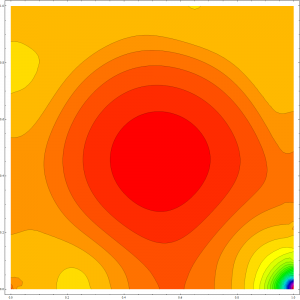
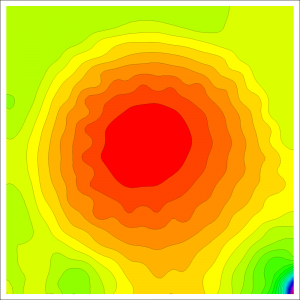
Jako základní model pro simulaci proudění v Kaplanově turbíně, který bude využit, byly zvoleny nestacionární Navier-Stokesovy rovnice. Jedná se o časově závislé nelineární parciální diferenciální rovnice, které jsou, jak již bylo zmíněno, numericky řešeny pomocí isogeometrické analýzy. Jako vhodný model pro časovou diskretizaci úlohy byla zvolena tzv. metoda štěpení, která při vhodné volbě parametrů poskytuje bezpodmínečně stabilní metodu vyššího řádu. V roce 2013 se řešitelský tým zaměřil na implementaci a testování 2D případu. K řešení nestacionárních Navier-Stokesových rovnic je ale nezbytné studovat i zjednodušené úlohy, jako je Stokesova úloha nebo stacionární Navier-Stokesova úloha. V rámci řešení projektu tak vznikla funkční implementace řešiče v softwaru Wolfram Mathematica všech tří výše zmíněných úloh, která byla otestována na řadě standardních testovacích příkladů a výsledky byly porovnány se známými výsledky těchto úloh. Na následujících obrázcích je možné vidět výstup z implementace pro standardní testovací úlohu – proudění ve čtvercové kavitě. Konkrétně jsou zobrazeny proudnice (vlevo a uprostřed) a rozložení tlaku (vpravo).
Při řešení testovacích úloh se projevil další ze známých faktů — pro prudce se měnící data dochází k destabilizaci numerického řešení. Z řady známých postupů, které bylo prostudovány, byla zvolena metoda SUPG (Streamline Upwind Petrov Galerkin), která se v případě využití pro stabilizaci numerického řešení Navier-Stokesových rovnic doplňuje o metodu PSPG (Pressure Stabilized Petrov Galerkin). Numerické řešení rovnic včetně stabilizace bylo opět implementováno v prostředí Wolfram Mathematica a příklad výstupu pro Reynoldsovo číslo Re=50000 získaný na poměrně hrubé síti (20×20 prvků) je zobrazen na následujících obrázcích.
V případě vyšších Reynoldsových čísel (což je i náš případ simulace proudění ve vodních turbínách) je nezbytné doplnit matematický model proudění o popis turbulentního chování tekutiny, což dále komplikuje numerický model. Opět byla provedena rozsáhlá analýza existujících metod a analyzovány vhodné metody pro tento případ. V našem případě se jako vhodný model jeví RANS metody, kde hlavní princip spočívá v tom, že Navier-Stokesovy rovnice jsou průměrovány v časovém intervalu. V rovnici se tak objeví další člen, který se aproximuje speciálními postupy pro numerické modelování — v našem případě byl jako optimální zvolen k-ω model, který rozšiřuje numerický model o další dvě parciální diferenciální rovnice pro tzv. turbulentní kinetickou energii k a specifickou disipaci ω. Doplněné rovnice mohou mít advekčně-difúzní charakter a na jejich řešení je nutné uplatnit podobný aparát jako na Navier-Stokesovy rovnice (aproximace řešení, stabilizace, linearizace atd.). V minulém roce byly zahájeny práce na implementaci k-omega modelu jako doplnění numerického modelu.