V rámci projektu TA03011157 byla navžena a implementována metoda pro návrh a optimalizaci lopatek obežných kol Kaplanovy a Francisovy turbíny. Metoda je založena na využití negradientní metody hejna a využívá v projektu implementované metody pro generování plošných a objemových B-spline modelů těchto typů turbín a isogeometrického řešiče simulace proudění.
Pro tvarovou optimalizaci Kaplanovy turbíny se využívá dvou typů geometrických modelů:
- B-spline model hydraulického profilu turbíny s rozváděcími lopatkami, ale bez lopatek oběžného kola,
- B-spline model oběžného kola.
U Francisovy turbíny je potom B-spline model hydraulického profilu bez lopatek oběžného kola nahrazen B-spline modelem rozváděcího kola. Vždy je nejprve proveden inicializační simulace proudění v hydraulickém profilu bez lopatek oběžného kola u Kaplanovy turbína, resp. v rozváděcím kole u Francisovy turbíny. Cílem tohoto výpočtu je získat rychlostní pole za rozváděcími lopatkami. Následně je vygenerován inicializační tvar lopatky oběžného kola a spuštěna vlastní optimalizace. Ta je založena na metodě hejna. Je tedy vygenerován zvolený počet perturbovaných geometrií lopatky oběžného kola, které se liší volbou designových parametrů. Pro každou geometrii je provedena simulace proudění v oběžném kole pomocí isogeometrického řešiče a vyhodnocena cílová funkce. Ze všech geometrií je vybrána nejlepší geometrie vzhledem k hodnotě cílové funkce a také jsou pro každou geometrii porovnány současné hodnoty cílové funkce s dosud nejlepší geometrii. Na základě toho je určena pro každou geometrii změna designových parametrů. Dále se již cyklus opakuje – pro modifikované designové parametry jsou vygenerovány plošné a objemové B-spline modely oběžných kol, provedeny simulace proudění, vyhodnocení cílové funkce atd.
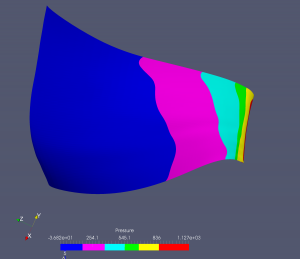
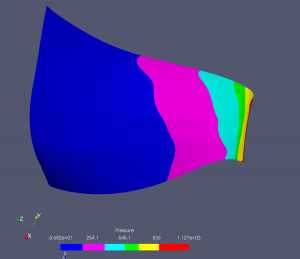
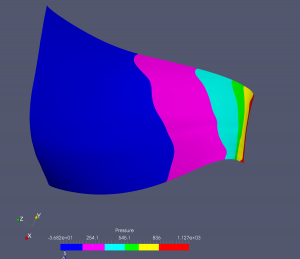
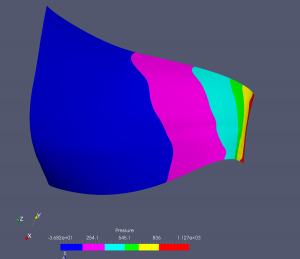
Ukažme si pro každý typ turbín jeden příklad běhu optimalizačního cyklu. V případě Kaplanovy turbíny je numerická simulace proudění prováděna na B-spline výpočetních sítích, které mají typicky kolem 2000 B-spline elementů, v níže prezentovaném případě to bylo 1760 B-spline elementů. Jen upozorněme, že nelze přímo srovnávat počty elementů použitých při isogeometrické analýze a např. při použití metody konečných prvků nebo objemů. U isogeometrické analýzy je typicky možné dosáhnout kvalitativně obdobných výsledků při řádově nižším počtu elementů, obvykle 10x – 100x menším. Níže uvedené obázky ukazují tlakové rozložení na lopatce oběžného kola Kaplanovy turbíny v různých iteracích optimalizačního cyklu.
Přetlaková strana lopatky:

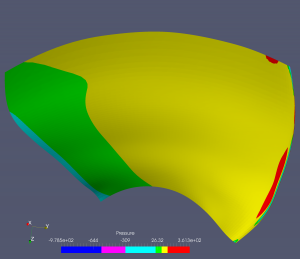

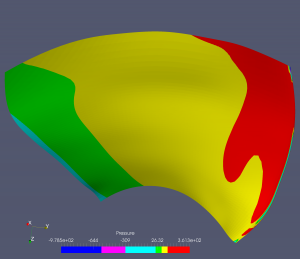
Podtlaková strana lopatky:




Metoda probíhá analogicky i pro Francisovu turbínu. Proto si zde opět ukážeme pouze výsledky jednoho konkrétního běhu optimalizačního procesu.
Vysokotlaká strana lopatky:


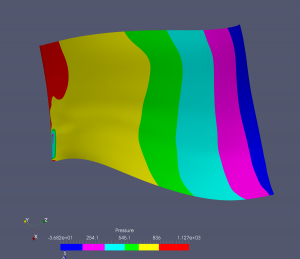
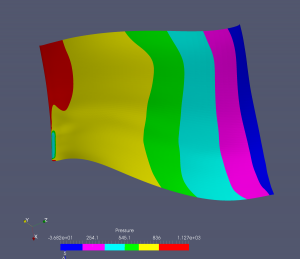
Nízkotlaká strana lopatky: